Sample Mislabeling and Boosted Trees
A while back, I saw this post on StackExchange/Crossvalidated: “Does anyone know how well C5.0 boosting performs in the presence of mislabeled data?” I did some simulations in order to make a comparison with gradient boosting machines (GBM).
Some publications simulate mislabelling by sampling from distinct multivariate distirbutions for each class. I simulated two class data based on this post. Each simulated sample has an associated probability of being in class #1. A random uniform number is generated to assign each sample and observed class label. To mislabel X% of the data, a random set of samples are selected and the probability of being in class #1 is reversed.
Simulated data sets were simulated with training set sizes between 100 and 1000. The amount of mislabeled data also varied (at 5%, 10%, 15% and 20%). For each mislabeled data set, there is a matched training set (form the same random number seed) with no intentional mislabeling. For each of these configurations, 500 simulations were conducted.
Model performance was assessed using the area under the ROC curve. A test set of 10,000 with no mislabeling was used to evaluate performance.
For the C5.0 and GBM models, models were tuned using cross-validation. For each technique, a model was trained on the mislabeled data and another on the correctly labeled data. In this way, we have a “control” model that reflects how well the model does for each data set if there were no added noise due to mislabeling. As a result, for C5.0 and GBM, a percentage of performance loss can be calculated against the correctly labelled control set:
pct = (mislabeled - correct)/correct*100). This image contains the distributions of the percent loss across the configurations:
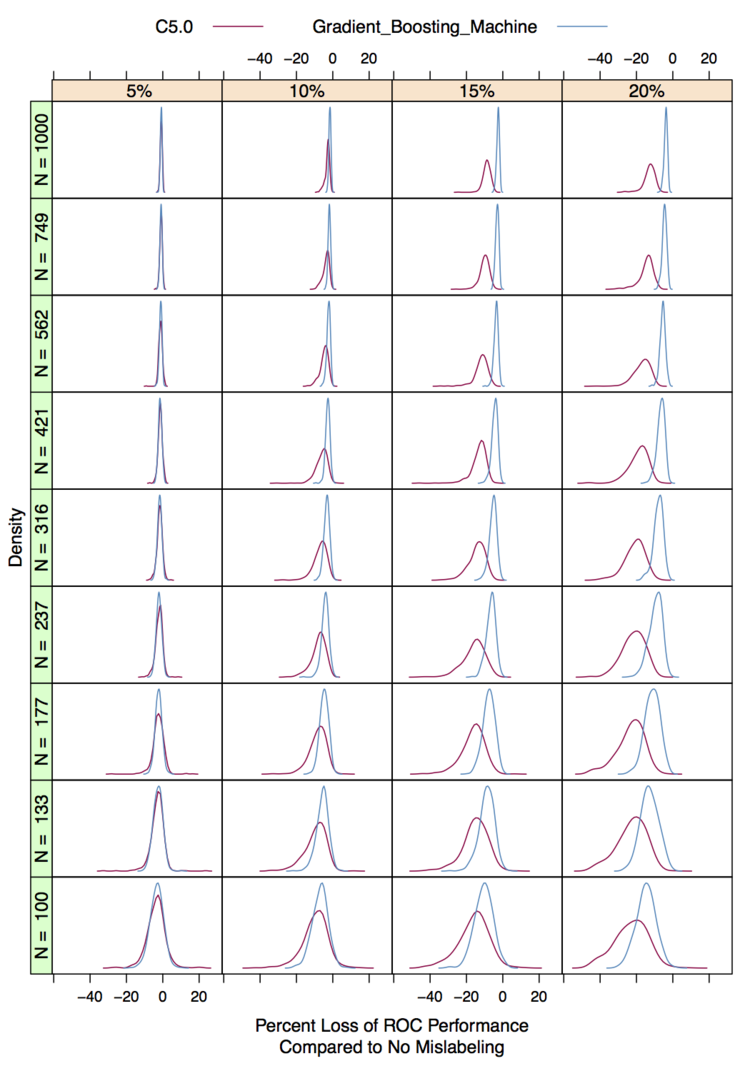
Some other observations:
- When there is no mislabeling, the results are almost identical
- Small amounts of mislabeling do not hurt either model very much
- The loss of performance decreases with training set size
- With gross amounts of mislabeling, the gradient boosting machine is not affected as much as C5.0
- The effect of mislabeling on C5.0 also impacts the variation in the results. If you compare the columns above, note that the C5.0 distribution does not simply shift to the left with the same level of variation.
I contacted Ross Quinlan about this and his response was:
“I agree with your conclusions for the function that you studied. My experiments with noise and AdaBoost suggested that the effect of noise (mislabeling) varies markedly with different applications. There are some summary results in the first part of the following:
I have only some vague ideas about why thus might be. For those applications where the classes are well-separated in the attribute space, mislabeling does not seem to alter the class clusters much. Alternatively, for applications where there is a tight boundary between two classes, mislabeling could markedly affect the perceived class divide.”
(This article was originally posted at http://appliedpredictivemodeling.com)